Seguro que han leido alguna vez esta frase:

  • Hay 10 tipos de personas, las que saben contar en binario y las que no

Evidentemente si no se sabe contar en binario parece una tontería, un error ó un chiste que no se entiende. Resulta muy técnico geek eso de decir que sabes contar en binario, y sin embargo es muy fácil y dá lugar a un juego de magia con cartas con el que asombrar a tus amigos durante el postre.

Un número binario es una secuencia de 1 (unos) y O (ceros). De acuerdo a la posición que ocupen toma un valor, y este valor siempre será doble del valor que le precede. Mejor con ejemplos:

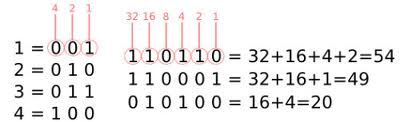
En rojo el valor que toma cada dígito. Este valor se tiene en cuenta en la suma si está encendido (1) y se ignora si está apagado (0). (Los ceros a la izquierda se pueden ignorar, pero para facilitar la comprensión los he mantenido ).

Según esto, resulta facil ver que en binario harian falta 6 digitos para contar desde 1 a 63, simplemente combinando 1 y 0 (el numero 64 correspondería al 7 digito encendido), siendo 63 el representado por 111111 = 32+16+8+4+2+1 = 63.

Con 7 digitos contariamos hasta 128, con 8 hasta 256. (seguro que más de uno ya está viendo relaciones entre estos números, su memoria RAM ó su paleta de colores). Bueno, pues ya sabes contar en binario. Vamos al juego

Las cartas

Para facilitar la explicación haremos el juego con solo 5 cartas. Al final verás que es muy facil hacerlo con tantas cartas como quieras.

Según lo visto anteriormente, usando 5 digitos binarios podriamos contar desde 1 a 31, combinando 1 (unos) y 0 (ceros) en distintas posiciones de tal manera que la suma de sus valores nos dá el numero decimal en cuestión. ¿si?

Bien, imagina que tenemos 5 cartas (en tu caso 5 servilletas valen) y un bolígrafo. En la primera servilleta vamos a escribir, de esos 31 numeros, aquellos que en codificación binaria tengan un valor de 1 en la 1ª posicion. En la segunda servilleta aquellos que en 2ª posición tengan un 1. En la tercera servilleta aquellos que en 3ª posición tengan un 1, etc…. Empezaría así la serie:

  • 1 = 00001 => primera servilleta

  • 2 = 00010 => segunda servilleta

  • 3 = 00011 => primera y segunda servilleta

  • 4 = 00100 => tercera servilleta

  • 5 = 00101 => tercera y primera servilleta

  • 6 = 00110 => tercera y segunda servilleta

  • etc….

Despues de repartir los 31 números deberían quedarte 5 servilletas garabateadas asi:

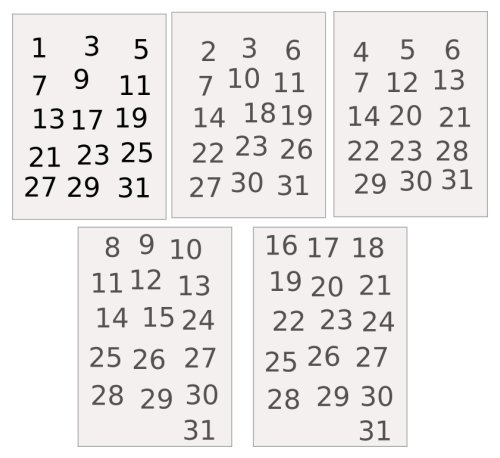
Pues ya tienes tu juego preparado, actua un poco y haz lo siguiente:

  • Escoje a tu victima

  • Dile que piense en un número cualquiera entre 1 y 31

  • Cuando lo tenga, dale las servilletas y dile que se quede con aquellas en que aparece su número.

  • Para averiguar su número, echa un vistazo rápido a sus servilletas y suma el primer numero de cada una de ellas, el resultado es su número.

  • Si te dice que está en todas, no sumes: es el 31

  • Si solo está en 1 servilleta, puede ser el 1, 2, 4, 8 ó 16

Básicamente lo que hemos hecho es descomponer en conjuntos los primeros 31 números decimales basandonos en su codificación binaria. Cada servilleta representa un dígito. Si el usuario selecciona una servilleta cualquiera, lo que nos está diciendo es que esa posición de la codificación binaria está encendida (es un 1). Así, si selecciona la última servilleta, nos está diciendo que su número es 10000 , es decir 10000 = 16. Si selecciona la última y la primera, nos está diciendo que la codificación binaria del numero elegido es 10001 = 16+0+0+0+1 = 17.

Si quieres darle más magia al asunto, podrías enseñarle las servilletas y dejar que él las escoja. No tienes ni que mirarlas, bastaría con enseñarselas de forma ordenada y fijarte en las que escoje para saber de que número se trata.

Facil, ¿no? Si quieres complicar el asunto puedes añadir un sexto digito (otra servilleta) y alargar tu capacidades adivinatorias hasta el 63, o dos servilletas y llegar hasta el 127.

Con esto y toque a lo Juan Tamariz triunfas seguro.